4.3 Graph with Intercepts
- Identify the $x$- and $y$-intercepts on a graph
- Find the $x$- and $y$-intercepts from an equation of a line
- Graph a line using the intercepts
Assignment
Identify the $x$- and $y$-Intercepts on a Graph
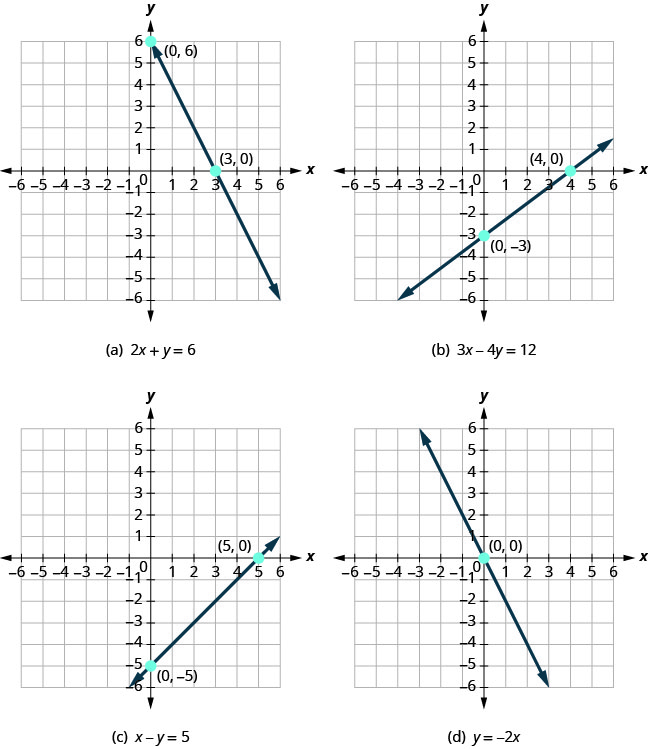
It’s good practice to use three points to graph a line, just to make sure there are no mistakes, but you technically only need two. Two convenient points are the intercepts, where the line crosses the $x$- and $y$-axis.
Figure 4.3.1 Some equations, their lines and their intercepts.
These points are visually convenient because it’s usually easy to spot where they cross each axis. And they are numerically convenient because one of the coordinates is $0$.
- An $x$-intercept crosses the $x$-axis at a point where the $y$-coordinate is $0$.
- A $y$-intercept crosses the $y$-axis at a point where the $x$-coordinate is $0$.
Finding and Graphing Intercepts from an Equation
Finding intercepts from an equation involves using the $0$ rule from above. If you want to find the $x$-intercept, plug a $0$ in for $y$. If you want the $y$-intercept, plug $0$ in for $x$.
\[\begin{align} 2x + y &= 6 \\[1em] 2(0) + y &= 6 \\ y &= 6\\[1em] 2x + (0) &= 6 \\ x &= 3 \end{align}\]For the equation above, your $y$-intercept is $(0,6)$ and the $x$-intercept is at $(3,0)$.
To graph, plot those two points, and then do one more. Finding a third point is still best practice for making sure you get a proper line from the equation. For this equation, plugging in $1$ yields $y=4$, so $(1,4)$ is our third point.