6.4 Logarithmic Functions
- Graph logarithmic functions and interpret their key features.
- Write and interpret the inverses of exponential and logarithmic functions.
Assignment
- p325 7–12, 15–31 (pdf)
- Answers to odd questions / even questions
Additional Resources
Key Features of Logarithmic Functions
It will likely come with little shock that logarithmic functions are the inverse function of exponential functions.
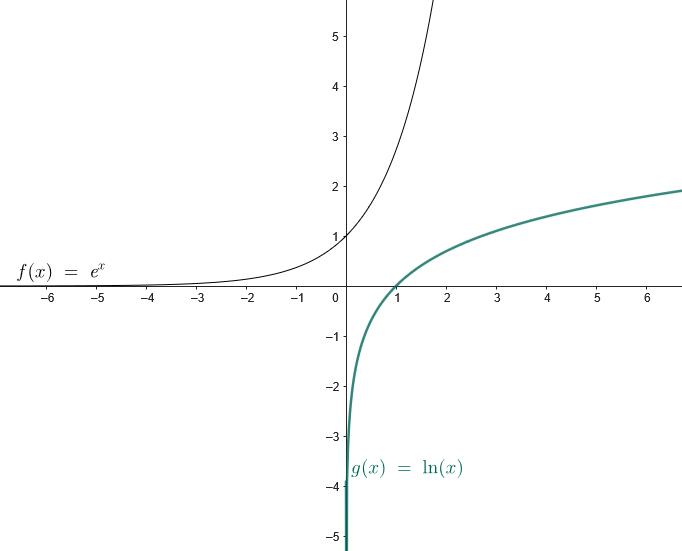
Figure 6.4.1 Graph of $e^x$ and $\ln{x}$.
- While exponential functions have domain of all real numbers, logarithmic functions have a range of all real numbers.
- An exponential has a range of $y\ge0$, and a logarithmic has a domain of $x \ge 0$.
- The $y$-intercept in an exponential function becomes an $x$-intercept in a logarithmic function.
- Logarithmic functions have a vertical asymptote at $x=0$.
-
End behavior is below.
\[\begin{align} \lim_{x\to\infty}f(x)=\infty \qquad \lim_{x\to0^+}f(x)=-\infty \end{align}\]I don’t think I’ve shown you limit notation yet, but for the sake of exposure, there it is. As $x$ heads towards infinity, $f(x)$ also goes to infinity. And as $x$ heads towards $0$ from the right, $f(x)$ goes to negative infinity.
The Rest of the Section
-
Transformations can be applied and follow the same rules as with other functions: adding results in translations, multiplying is scaling, and where you add or multiply will determine if it’s horizontal or vertical. Here is a Desmos graph that will allow you to try out all the different transformations.
-
If you need to invert a logarithm, there’s no need to restrict the domain since it’s one-to-one, meaning there’s no repeat $y$-values. Just solve for $x$, then adjust your variables accordingly.
\[\begin{align} y & = 10^{x+1} \\ \log y &= x + 1 \\ -1 + \log y &= x \\[1em] \end{align}\] -
Average rate of a change comes up again. That is just slope by another name, so find $\frac{\Delta y}{\Delta x}$, or the change in $y$ over the change in $x$.