1.1 A Preview of Calculus
- Understand what calculus is and how it compares with precalculus.
- Understand that the tangent line problem is basic to calculus.
- Understand that the area problem is also basic to calculus.
Assignment
- Vocabulary and teal boxes
- p63 5, 6, 10, 13, 16, 17, 19, 20 22–24
The vertical bar indicates the AP cut-off. Problems after the bar are recommended for AP prep, but not required for the assignment.
Additional Resources
- AP Topics: 1.1
Calculus is the mathematics of change.
- An object traveling at a constant velocity can be analyzed by precalculus math (not Precalculus, just before calculus). For an accelerating object you need calculus
- Slope of lines is also precalculus. Slopes of curves is calculus.
- The area of rectangles and other polygons is precalculus. The area under a curve requires calculus.
The book provides more examples of things you can do with the math you’ve already been taught, and what you’ll be able to do once you have calculus added to your tool belt. And the big precursor to all this is limits.
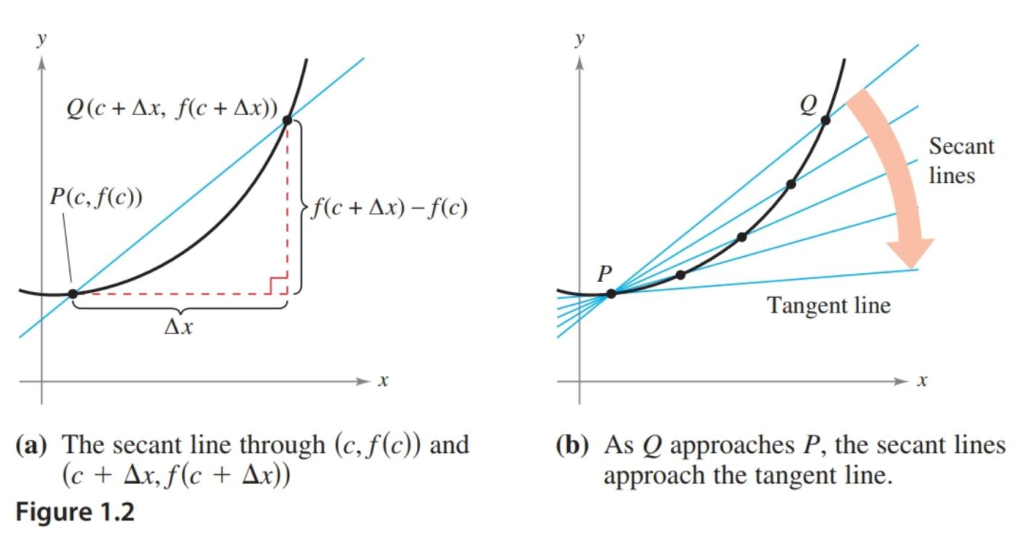
The Tangent Line Problem
You’ve already learned how to find the slope of secant lines, lines which are lines that cross a curve at two points. This is the same as your average rate of change.
Calculus focuses on finding the slope of tangent lines, where the line only crosses the curve at a single point. Imagine a secant line, but then move one point closer and closer to the other. When those points are the same, you have a tangent line. And the value that the slope approaches is its limit.
Here is the Desmos demo I showed in class.
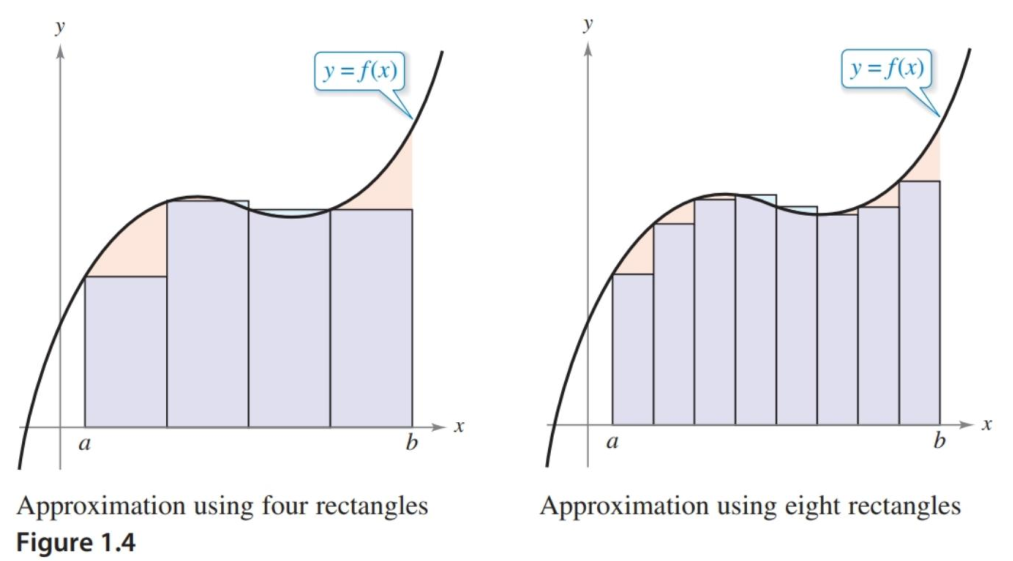
The Area Problem
As a second example of limits in action, imagine trying to find the area under a curve, like the one pictured below. A good way to start is by breaking the area into rectangles, and adding up those areas.
But, its not terribly accurate with a small number of rectangles. You can more to get a more accurate result, but there will still be gaps. If you push this idea to its limit of an infinite number of rectangles, you’ll get the precise area under the curve.
Here is the Geogebra demo I showed in class.