Kurzius Math Notes

2.2 Basic Differentiation Rules and Rates of Change

AP Topics: 2.1, 2.5, 2.6, 2.7, 4.1, 4.2

✎ p144 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 41, 49–51, 54–72 even, 73, 75, 82, 85 | 94, 96, 100–109, 119–122

Last section, we saw that we could either find the slope of the tangent line at specific points along a function, but we could also generalize and find the derivative of the function, allowing us to plug in $x$-values to get the desired slope.

You’ll be happy to hear there is are faster ways to derive these derivatives, but maybe less happy to hear it involves lots of memorization. The bulk of this chapter will be going over all of these rules. Don’t worry, there are cheat sheets everywhere, including at the beginning of the book. I also put a copy on Canvas and here’s a link to same one just in case you don’t feel like logging in, but …

You will NOT get a reference sheet on the AP exam.

You also won’t get one on quizzes and tests in class. Use them as needed on homework, but ween yourself off as soon as possible.

A Note on Notation and Proofs

Last section, we saw $f’$ used heavily, and then briefly mentioned $\frac{dy}{dx}$, but now our focus will shift to the latter. The fuller story on this version is that $\frac{d}{dx}$ is an operation, so a more accurate way of writing it would be $\frac{d}{dx}y$. You’ll mostly see this version of the notation below in order to emphasize that action of performing an operation.

Also, most of these rules have accompanying proofs in the textbook. I will not be going through them here, but read them over and I might cover some in class depending on time.

Without further ado …

Derivative of a Constant Function

\[\frac{d}{dx}[c]=0\]

Hopefully this makes sense intuitively. Since the derivative function is the slope of the function, a constant function is a horizontal line with a slope of 0.

The Power Rule

\[\frac{d}{dx}[x^n] = nx^{n-1}\]

The derivative of $x^3$ is $3x^2$ and $x^{-4}$ is $-4x^{-5}$. We will likely go over this proof as reviewing expanding binomials is worth doing.

Constant Multiple Rule

\[\frac{d}{dx}[cf(x)] = cf'(x)\]

In other words, you can factor out a constant, then find your derivative like normal. Don’t forget that denominators count, too. There is no difference between $\frac{x^2}{5}$ and $\frac{1}{5}x^2$.

Sum and Difference Rule

\[\frac{d}{dx}[f(x) \pm g(x)] = f'(x) \pm g'(x)\]

If you see addition or subtraction, the derivative is the sum or difference of the two derivatives. The derivative of $3x^5 + 2x$ is $15x^4 + 2$.

Derivative of the Sine and Cosine Functions

\[\frac{d}{dx}[\sin x] = \cos x\]

With that rule in mind, take a look at the graph of $\sin x$ and $\cos x$ below.

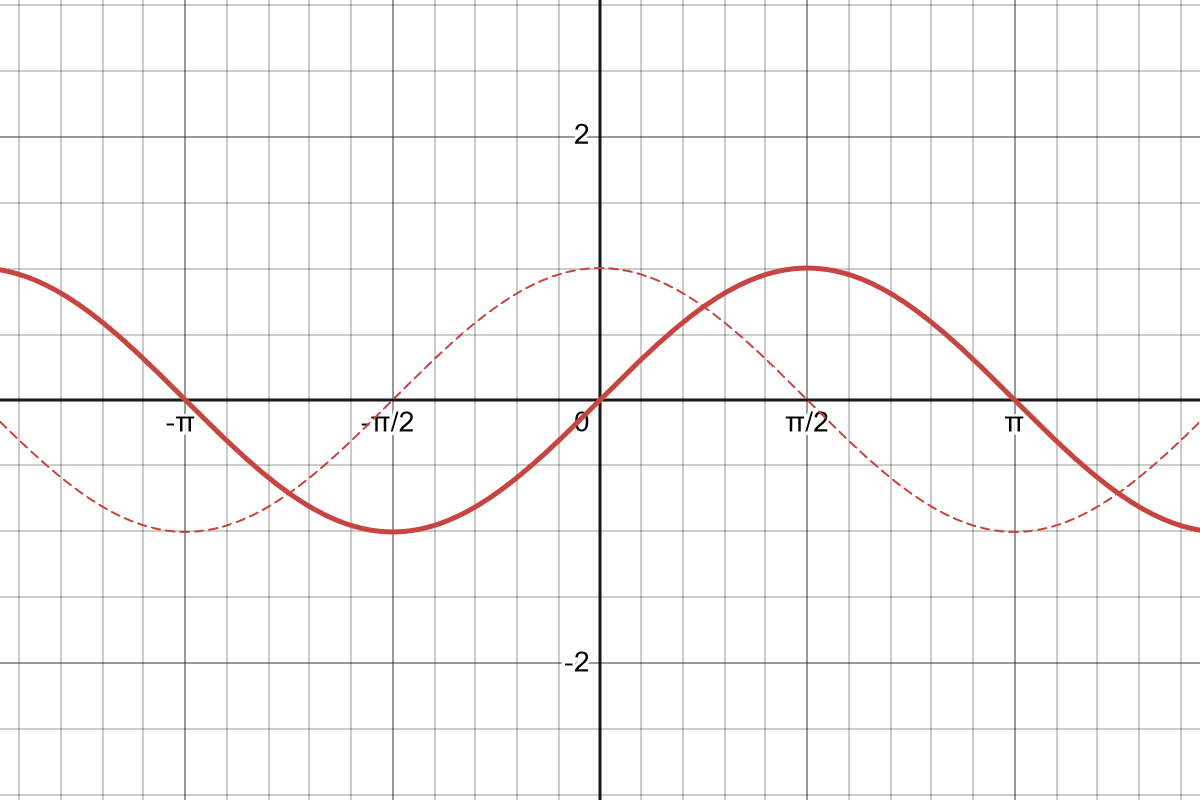
sin(x) and d/dx sin(x)

One of the more imporant things about derivatives is being able to connect it to slope graphically. So with that in mind,

  1. When $\sin x$ is increasing, what is true about $\cos x$? What about when it’s decreasing?
  2. When $\sin x$ switches from increasing to decreasing, what is true about $\cos x$?
  3. At those same places on $\cos x$, what appears to be the slope of $\sin x$?

You can try the same things above with $\cos x$ and you should arrive at the conclusions below.

\[\quad \text{and} \quad \frac{d}{dx}[\cos x] = -\sin x\]

Derivatives of Exponential Functions

The last rule covered in this section is for $e^x$. Good news, it’s an easy one.

\[\frac{d}{dx}\left[e^x\right] = e^x\]

Yep, $e^x$ is its own derivative.

Rates of Change

Derivatives give you slope at a point. Slope is the change in $y$ over the change in $x$., but that is when math exists in a vacuum. Applying this idea to real-world applications means derivatives can find the instantaneous rate of change of any two related variables.

A common pair of related variables is position and time, where comparing change in position to change in time gives you velocity. You’ve found average velocity before, but now with derivatives, you can find instantaneous velocity.

Free-Falling Objects

We will eventually see where the below equation comes from, but for now make sure you know how to use it.

Given acceleration due to gravity $g$, initial velocity $v_0$, and initial position $s_0$, the function for an object’s position when in free-fall is

\[s(t) = -\frac{1}{2}gt^2 + v_0t + s_0\]

Gravity on Earth is typically given as either $32 \text{ ft}/\text{s}^2$ or $9.8 \text{ m}/\text{s}^2$.

So, given a diver 32 feet up with an initial velocity of 16 feet per second, we can write our position function as

\[s(t) = -16t^2 + 16t + 32\]

From here, we can derive their velocity function, since $s’(t) = v(t)$.

\[v(t) = -32t + 16\]

Well, what if we wanted to know how fast they were traveling when they hit the water? First we need our zeros, which means solving the original position function for 0.

\[s(t) = -16t^2 + 16t + 32 = -16(t^2-t-2) = -16(t-2)(t+1)\]

Our zeros are 2 and -1, but only 2 makes sense in this context, they hit the water after two seconds. Now we can just plug into our velocity function.

\[v(2) = -32(2) + 16 = -48 \text{ ft}/\text{s}^2\]

Notice how the velocity is negative. Position can be positive or negative since we can move in opposite directions (you’ll also see left/right later on), so velocity will also tell you if the object is traveling in a positive or negative direction.

Just keep in mind that speed is the absolute value of velocity; direction is ignored when we just want to know how fast something is moving.