Kurzius Math Notes

1.3 Evaluating Limits Analytically

AP Topics: 1.2, 1.5, 1.6, 1.7, 1.8, 1.9

• Evaluate a limit using properties of limits.
• Develop and use a strategy for finding limits.
• Evaluate a limit using the dividing out technique.
• Evaluate a limit using the rationalizing technique.
• Evaluate a limit using the Squeeze Theorem.

✎ p84 2, ,6, 8, 9–25 odd, 29–32, 34-86 even, 95, 98 | 101, 104, 108, 113, 123–125

---

Last section, we saw examples where the value of a limit and its true value matched. For example, for $f(x)=x^2$.

\[\lim_{x\to2}f(2)= f(2)\]

The function appears to be approaching 4 when $x=2$, and it also is 2 when $x=2$.

For a vast number of functions and situations, substituting is a valid way to evaluate a limit, rather than using tables and graphs like was shown last section. The book walks you through the specifics on this, which I do suggest you read through.

There is one other theorem that addresses a situation we saw last section.

\[f(x) = \begin{cases} x^2+x + 1, & x\neq 1 \\ 1, & x=1 \end{cases} \qquad g(x)=x^2+x + 1\]

If two functions are identical save for a specific value, than its safe to assume their limits agree. So, despite the first case not being defined when $x=1$, we can still use $g(x)$ to determine $\lim_{x\to1}f(x)$.

A Strategy for Finding Limits

Simply put, substitute when you can. If you can’t see if there is another function that matches, even if the one value is excluded. This can involve rewriting your function or simplifying to find that function.

For both, graphs and tables will help to reinforce what you found, even if you could not find a limit.

Finding the Other Function

One way to find the almost equivalent function is by dividing when presented with a rational function.

\[\lim_{x\to -3} \frac{x^2+x-6}{x+3}\]

Substitution gives us $0/0$, also known as the indeterminate form, but $x-3$ is a factor of $x^2+x-6$.

\[f(x)=\frac{x^2+x-6}{x+3} = \frac{(x+3)(x-2)}{x+3}=x-2\]

We’ve found our equivalent function. Substituting $x=-3$ gives us a limit of $-5$.

As a reminder, the domain from the original carries over to the new function. Although $x-2$ can be evaluated when $x=-3$, as a function in this situation, it cannot. We are only using it to evaluate the limit. It might seem like a minor distinction, but it’s important to remember that the limit of a function is not the same as the value of the function.

---

Another technique is rationalizing radicals, meaning multiplying by a radicals conjugate.

\[\lim_{x\to0}\frac{\sqrt{x+1}-1}{x}\]

Multiplying by $\sqrt{x+1}+1$ will hopefully open up an avenue to find the limit.

\[\begin{align*} \frac{\sqrt{x+1}-1}{x} \cdot \frac{\sqrt{x+1}+1}{\sqrt{x+1}+1} &= \frac{(x+1)-1}{x(\sqrt{x+1}+1)} \\ &= \frac{x}{x(\sqrt{x+1}+1)} \\ &= \frac{1}{\sqrt{x+1}+1} \end{align*}\]

Again, as a function this still can be evaluated at 0, but for the purpose of finding a limit, this works. The limit is $1/2$.

The Squeeze Theorem

If a function is less than or equal to another, and a third lies in between them, whenever the bounding function have an equal limit, then the inner one shares the same limit.

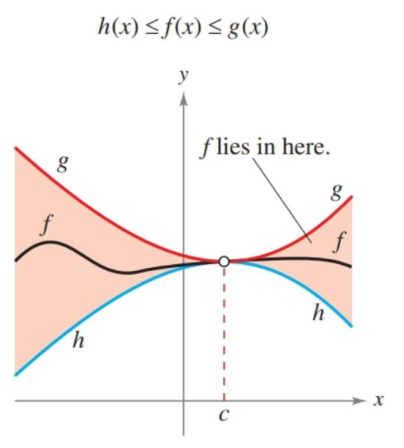
This is particularly helpful in proving some more difficult limits, like $\lim_{x\to0}\frac{\sin x}{x}=1$. There are two others limits listed that are proved using the squeeze theorem, which are helpful in solving other limits.

\[\begin{align*} \lim_{x\to0}\frac{\tan x}{x} &= \lim_{x\to0}\left(\frac{\sin x}{x}\right)\left(\frac{1}{\cos x}\right) \\ &= \lim_{x\to 0}\frac{\sin x}{x} \cdot \lim_{x\to 0}\frac{1}{\cos x} \\ &= 1\cdot 1 \\&=1 \end{align*}\]