4.2 Area
Lesson: February 6, 2025. Quiz: February 13, 2025.
- Use sigma notation to write and evaluate a sum
- Understand the concept of area
- Approximate the area of a plane region
- Find the area of a plan region using limits
Assignment
- Vocabulary and teal boxes
- p299 1, 4, 7–35 odd, 41, 45, 48, 53, 58, 61, 68, 69 75, 76, 78, 81–83
Additional Resources
- AP Topics: 6.1
- Khan Academy
Considering the time spent on antidifferentiation and integration last section, it’s going to appear like we’re going off-topic. Don’t worry, we’ll get back there soon enough.
Sigma Notation
We’re going to start off with some notation that’s used in summations, which is where you need to sum up a pattern of terms. Say we wanted to add up all the numbers from 1 to 10. Instead of writing it all out, we could instead write
\[\begin{align} \sum_{i=1}^{10} i \end{align}\]The $i=1$ tells us to start at 1, and the $10$ up top tells us the upper bound of the sequence. Another is below.
\[\begin{align} \sum_{i=4}^7 \frac{1}{i^2} &= \frac{1}{4^2} + \frac{1}{5^2} + \frac{1}{6^2} + \frac{1}{7^2} \\ &= \frac{1}{16} + \frac{1}{25} + \frac{1}{36} + \frac{1}{49} \end{align}\]Same story here, except we start at 4 and end at 7. We plug in for $i$ each time, which is now squared and in the denominator. The general form for this is below, where $a_i$ is used to represent the each term in the sequence.
\[\begin{align} \sum_{i=1}^n a_i = a_1 + a_2 + a_3 + \dots + a_n \end{align}\]There are a few formulas and rules listed under Theorem 4.2 that we’ll use when evaluating some summation. Memorizing them is helpful, but not required for the AP exam.
A few other things to keep in mind:
- If our term is being multiplied by a constant, we can factor it out, and then back in later.
- If two terms are being added or subtracted, we can evaluate them separately.
- If our term is just a constant, then $\sum_{i=1}^{n} c = cn$
With that knowledge, we can rewrite a sum like the one below so we can evaluate it easily.
\[\begin{align} \sum_{i=1}^{n} \frac{i+i}{n^2} &= \frac{1}{n^2} \sum_{i=1}^{n} (i+1) &&\text{Factor out the constant} \\[1.5em] &= \frac{1}{n^2} \left(\sum_{i=1}^{n} i + \sum_{i=1}^{n} 1\right) &&\text{Write as two sums} \\[1.5em] &= \frac{1}{n^2} \left(\frac{n(n+1)}{2} + n\right) &&\text{From Theorem 4.2 and 3 above} \\[1.5em] &= \frac{n+3}{2n} &&\text{Simplify} \end{align}\]Area
I recommend you read through what the book as written here. It does an excellent job of framing what’s coming up.
The Area of a Plane Region
Now, we’ll take this concept of summations and apply it to the areas underneath a curve. First, we’ll slice the area into rectangles, and then add up the areas of those rectangles.
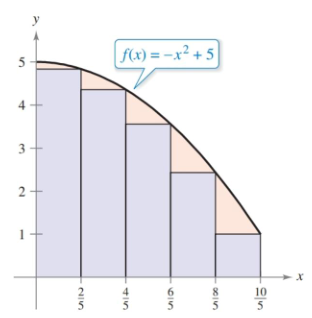
The first time through, we’ll use rectangles with their right-side touching the curve. The curve here is $-x^2 + 5$ on the interval $[0,2]$. Before we can construct our sum, we’ll need to figure out the width and height of each rectangle.
Width is straightforward. Our interval distance is two and we have five rectangles, each rectangle’s width is $2/5$.
In order to get the heights, which are our $y$-values, we’ll need the $x$-values for the right side of each rectangle. The width of each is the same and we know where the interval starts, so they are predictable. If you remember how to construct linear expressions, this is just $0+\frac{2}{5}i$.
Now we that we have an expression for our $x$-values, we can plug it into our function to generate our $y$-values (heights). To construct our summation, we state that our bounds are from 1 to 5, and the expression we are summing is the height multiplied by the width.
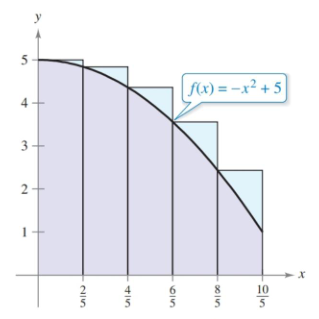
\[\begin{align} \sum_{i=1}^{5} \left[f\left(\frac{2}{5}i\right)\right]\left(\frac{2}{5}\right) = \sum_{i=1}^{5} \left[-\left(\frac{2}{5}i\right)^2+5\right]\left(\frac{2}{5}\right) \end{align}\]We can do the same for left endpoints with one little change. Since the left endpoints lag behind by one, our $f(2/5 \cdot i)$ becomes $f(2/5 \cdot (i-1))$.
Finding Area by the Limit Definition
So, we’ve explored summation notation and used it to approximate areas under curves. Now we’ll refine those approximations by defining the number of rectangles we’ll use as $n$, and then pushing that number to infinity.
First, we need to deal with some of the notation the book uses. So far, we’ve spoken in terms of left and right endpoints, but the book shifts to $f(m_i)$ and $f(M_i)$ to represent the smaller and larger rectangles that hit the curve. They also define width of each rectangle as $\Delta x$, so we end up with the equations below.
\[\begin{align} s(n) &= \sum_{i=1}^n f(m_i) \Delta x && \text{Area of rectangles inside the curve}\\ S(n) &= \sum_{i=1}^n f(M_i) \Delta x && \text{Area of rectangles outside the curve} \end{align}\]The true area will lie somewhere between those two approximations.
Let’s apply to this $x^2$ on the interval $[0,2]$. Since we are writing a summation based on $n$ rectangles, our width will be $\frac{2}{n}$ and our width is $f\left(\frac{2}{n}i\right)$. Since this curve is increasing on that interval, our right endpoints will the larger sum.
\[\begin{align} S(n) &= \sum_{i=1}^n f(M_i) \Delta x \\ &= \sum_{i=1}^n \left(\frac{2i}{n}\right)^2\left(\frac{2}{n}\right)\\ &= \frac{8}{n^3}\sum_{i=1}^n i^2 \\ &= \frac{8}{n^3} \left[\frac{n(n+1)(2n+1)}{6}\right]\\ & \dots \\ &= \frac{8}{3} + \frac{4}{n} + \frac{4}{3n^2} \end{align}\]The smaller sum is a similar process, except that since it involves the left endpoint, you’ll use $f(2(i-1)/n)$ instead.
Which sum corresponds to which endpoints will vary depending on the curve. Generally, increasing curves have the left endpoint as the smaller rectangle, and right endpoints are the smaller in decreasing curves. When a curve switches between the two … we’ll be doing this a different way by the time we get there.
Now that we can represent an approximation of the area for $n$ rectangles, what happens as $n$ approaches infinity? As the number of rectangles increases and their density under the curve becomes so high that their width all but disappears?
For one, it no longer matters which endpoint we use, as they essentially become the same. So, you can safely use the right endpoint (typically the easier of the two) to get your area.
Along with that, since $n\rightarrow\infty$, our terms with $n$ in the denominator become infinitely small, and can be ignored. In the example above, our sum was $\frac{8}{3} + \frac{4}{n} + \frac{4}{3n^2}$. Since $n$ is approaching infinity, those terms essentially become 0 and we are left with $\frac{8}{3}$.
Let’s tackle a slightly more difficult problem now that we have a new approach. Let $f(x) = 4 - x^2$ and our interval will be $[1,2]$. Notice that we are not starting at 0. That will affect our $x$-values for the function.
\[\begin{align} \text{Area} &=\lim_{n\to\infty} \sum_{i=1}^n f\left(1+\frac{i}{n}\right)\left(\frac{1}{n}\right) \\ &= \lim_{n\to\infty} \sum_{i=1}^n \left[4 - \left(1+\frac{i}{n}\right)^2\right]\left(\frac{1}{n}\right) \\ &= \lim_{n\to\infty} \sum_{i=1}^n \left(3-\frac{2i}{n}-\frac{i^2}{n^2}\right)\left(\frac{1}{n}\right) \\ &= \lim_{n\to\infty} \left[3-\left(1+\frac{1}{n}\right)-\left(\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}\right)\right] \\ &= 3 - 1 - \frac{1}{3} = \frac{5}{3} \end{align}\]Region Bounded the $y$-Axis
When you run into problems where we want area bounded by a function of $y$ instead of $x$, nothing actually changes. You still divide your interval by $n$ to get the width, and then multiply that by $i$ to get the summation terms.
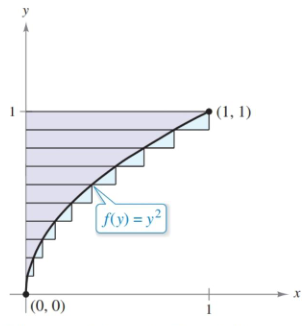
Approximating with midpoint
The last part of the section deals with approximating with midpoint, instead of the left or right endpoint. Your $i$ terms will now be the average of the left and right endpoints.
\[\begin{align} \sum_{i=1}^n f\left(\frac{x_{i-1} + x_i}{2}\right)\Delta x \end{align}\]