Lesson: January 28, 2025. Quiz: February 13, 2025.

  • Understand the concept of a tangent line approximation.
  • Compare the value of the differential, dy, with the actual change in y, Δy.
  • Estimate a propagated error using a differential.
  • Find the differential of a function using differentiation formulas.

Assignment

  • Vocabulary and teal boxes
  • p272 3–5, 9, 11, 14, 16–19, 25–28, 35 40, 52–55

Additional Resources

Tangent Line Approximations

Zoom in a part of a function’s graph enough and it will begin to look like a line. We can use that fact to estimate the value of a function. Instead of getting the function’s actual value, we can calculate the tangent line at a nearby convenient point and use that to estimate the function’s value at the point in question.

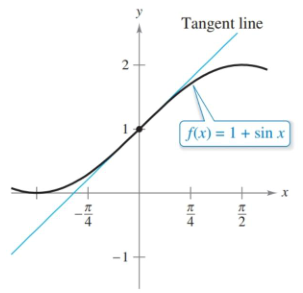
Tangent line approximation

If we use the point $(0,1)$ on the function $f(x)=1+\sin x$ we get a line with the equation

\[\begin{align} y &= f'(0)(x - 0) + f(0) \\ &= (\cos0)(x) + 1 \\ &= x + 1 \end{align}\]

Now, rather than having to evaluate $f(x)$, we can use our line to get values that will be very close to the true value of $f(x)$. Keep in mind that this will only be effective for values close to the $x$ we chose, which was $x=0$ in this case. Go to far and the estimates will be poor.

Differentials

The equation in $(1)$ can be generalized as

\[\begin{align} y = f(c) + f'(c)(x-c) \end{align}\]

where $c$ is value to be used for the estimate and $x$ the value you want to estimate. We’re going to change the way we look at this equation in two ways.

  1. $f(c)$ is our original $y$, so that means $f’(c)(x-c)$ is the change in $y$, which we’ll refer to as $dy$
  2. $x-c$ is the change in our $x$-value, which we can refer to as $dx$

This means we can write

\[\begin{align} dy = f'(x)dx \end{align}\]

meaning if we want to determine a small change in $y$, we need to multiply the small change in $x$ by the derivative of $f(x)$. This is our definition of a differential.

Equation $(5)$ will seem a bit strange since we know from derivative notation that $f’(x) = \frac{dy}{dx}$, but we unfortunately can’t make that leap in logic since $dy/dx$ isn’t technically a fraction. It often behaves like it, but it is not.

OK, let’s find a differential. Let $y=x^2$, $x=1$, and $dx=0.01$.

\[\begin{align} dy &= f'(x)dx \\ &= 2x \cdot dx \\ &= 2(1) \cdot 0.01 = 0.02 \end{align}\]

Keep in mind these are still estimates. You can compute the actual difference and compare them. In our book, $\Delta y$ and $\Delta x$ are used to represent actual change, while $dy$ and $dx$ are for differentials or estimates.

\[\begin{align} \Delta y &= f(x + \Delta x) - f(x) \\ &= (x+\Delta x)^2 - x^2 \\ &= (1.01)^2 - 1^2 \\ &= 1.0201 - 1 = 0.0201 \end{align}\]

Calculating Differentials

The book spends some time rewriting derivative rules in differential form and it’s worth a look through. Here though, I want to focus on approximating function values. The example in the book asks you to estimate $\sqrt{16.5}$. If we let $y=\sqrt{x}$, $x=16$, and $dx=0.5$ we should be able to get a decent approximation.

\[\begin{align} dy &= f'(x)dx \\ &= \frac{1}{2\sqrt{x}}dx \\ &= \frac{1}{2\sqrt{16}}\cdot\frac{1}{2} && \text{Fractions > decimals} \\ &= \frac{1}{16} \end{align}\]

If our $dy$ is $1/16$, then the approximation of $\sqrt{16.5}$ must be $(\sqrt{16}+dy)$ or $(4 + \frac{1}{16})$. If you know your decimals, this is $4.0625$, which is pretty close to the actual value of approximately $4.0620$.